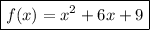Step-by-step explanation:
PART 1.
A quadratic function is given by the form:
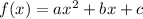
While a linear function is given by:
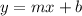
In this case, we have 2 cases:
CASE 1
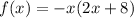
Applying distributive property we get:
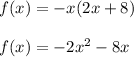
So this is a quadratic function.

CASE 2
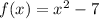
So this is a quadratic function.

PART 2.
Remember that for a quadratic function we have:
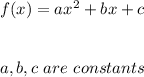
From the table:
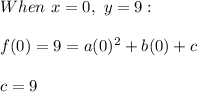
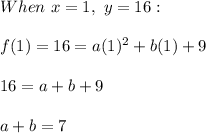
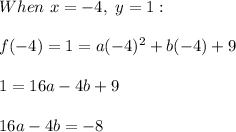
Solving for a and b:
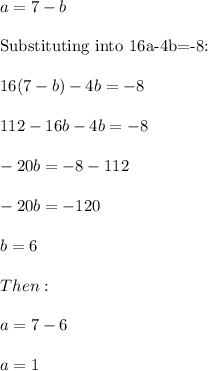
So the equation is: