Question

A spring is compressed 0.085 m and has a spring constant of 348 N/m. How

much work is in compressing the spring?
Use Hooke's Law.
Include, at most; 3 decimal places.

Answer 1

Work done to compress the string is 1.25715 J

Step-by-step explanation:

Given:

The spring is compressed to a distance x=0.085 m

Spring constant k=348N/m

To Find:

Work required to compress the string.

Solution:

According to Hooke's law, the force required to compress a string to a distance is given by

F= -kx

Thus expression for work done to compress a spring by a distance x can be calculated as,

`W=1/2 kx^2\\\\=1/2* 348* 0.085^2\\\\=1.25715J`

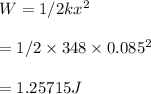
Thus the amount of work done to compress the string is 1.25715 J