Question

Is my answer correct or no?
---> show explanation & details if i am wrong!!!

Answer 1

No, because the distance from the origin to point (7 , -7) is greater than the radius of the circle ⇒ 3rd answer

Explanation:

From the graph of the circle

∵ The center of the circle F is at the origin

∴ F is (0 , 0)

∵ The circle passes through point (7 , 0)

- The length of the radius of the circle is the distance between

the center of the circle and a point on the circle

∴ r is the distance between points (0 , 0) and (7 , 0)

∴
`r=\sqrt{(7-0)^(2)+(0-0)^(2)}=√(49)=7`

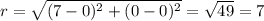
∴ The length of the radius of the circle is 7 units

Let us find the distance between point (7 , -7) and the origin (0 , 0)

• If the distance is equal to the radius of the circle, then the point is on the circle
• If the distance is greater than the radius, then the point is outside the circle
• If the distance is less than the radius, then the point is inside the circle

∵ The distance =
`\sqrt{(7-0)^(2)+(-7-0)^(2)}=√(49+49)=√(98)=7√(2)`

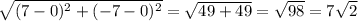
∵ r = 7

∵
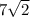`7√(2)` > 7

∴ The distance is greater than the radius of the circle

∴ Point (7 , -7) lies outside the circle

The correct answer is:

No, because the distance from the origin to point (7 , -7) is greater than the radius of the circle

Your answer is not correct, the correct answer is the 3rd answer