Answer:
5.5 N at 50.8° north of west.
Step-by-step explanation:
To find the resultant of these forces, we have to resolve each force along the x- and y-direction, then find the components of the resultant force, and then calculate the resultant force.
The three forces are:
 (east)
(east)
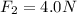 (west)
(west)
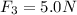 (at 60° north of west)
(at 60° north of west)
Taking east as positive x-direction and north as positive y-direction, the components of the forces along the 2 directions are:
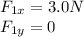
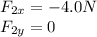
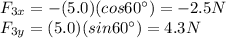
Threfore, the components of the resultant force are:
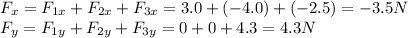
Therefore, the magnitude of the resultant force is
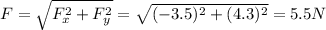
And the direction is:

And since the x-component is negative, it means that this angle is measured as north of west.