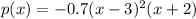Question

The polynomial of degree 3, P(x), has a root of multiplicity 2 at x = 3 and a root of multiplicity 1 at x = -2. The y-intercept is y=-12.6

Answer 1

`p(x) = - 0.7(x - 3)^(2) (x + 2)`

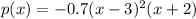
Explanation:

We have that the polynomial, has a root of multiplicity 2 at x = 3 and a root of multiplicity 1 at x = -2.

This means the factored form of the polynomial will be.

`p(x) = a(x - 3)^(2) (x + 2)`

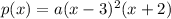
Also, it was given that, the y-intercept is y=-12.6.

This implies that:

`- 12.6= a(0 - 3)^(2) (0 + 2)`

`- 12.6= a(- 3)^(2) (2)`

`- 12.6= 18a`

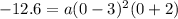
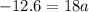
Divide both sides by 18;

`a = ( - 12.6)/(18)`

`a= - 0.7`

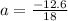
Therefore the polynomial is

`p(x) = - 0.7(x - 3)^(2) (x + 2)`