Answer:
Option A: b must equal 7 and a second solution to the system must be located at the point (2, 5)
Explanation:
The complete question is
Tom determines that the system of equations below has two solutions, one of which is located at the vertex of the parabola.
Equation 1: (x – 3)2 = y – 4
Equation 2: y = -x + b
In order for Tom’s thinking to be correct, which qualifications must be met?
A: b must equal 7 and a second solution to the system must be located at the point (2, 5).
B: b must equal 1 and a second solution to the system must be located at the point (4, 5).
C: b must equal 7 and a second solution to the system must be located at the point (1, 8).
D: b must equal 1 and a second solution to the system must be located at the point (3, 4).
step 1
Find the vertex of the quadratic equation
The general equation of a vertical parabola in vertex form is

where
(h,k) is the vertex
we have
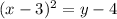
so
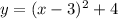
The vertex is the point (3,4)
step 2
Find out the value of b in the linear equation
we know that
If the vertex is a solution of the system of equations, then the vertex must satisfy both equations
substitute the value of x and the value of y of the vertex in the linear equation

For x=3, y=4
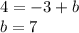
so
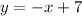
step 3
Find out the second solution of the system of equations
we have
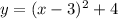 -----> equation A
-----> equation A
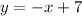 ----> equation B
----> equation B
solve the system of equations by graphing
Remember that the solutions are the intersection points both graphs
The second solution of the system of equations is (2,5)
see the attached figure
therefore
b must equal 7 and a second solution to the system must be located at the point (2, 5)