Answer:
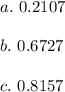
Explanation:
a. Our random variable follows a binomial distribution which is defined as:
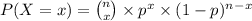 where
where
 is the probability of success,
is the probability of success,
 the sample size and
the sample size and
 the random variable.
the random variable.
-Given that
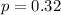 ,
,
 what's
what's

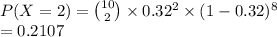
Hence, the probability of exactly two is 0.2107
b. The probability that more than two adults are more likely to make purchases during a sales tax holiday is given by:
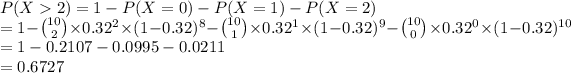
Hence the probability of more that two adult purchases is 0.6727
c. The probability that the number of adults who say they are more likely to make purchases between 2 and 5 is obtain by summing the the probabilities
p(x=2)+p(x=3)+p(x=4)+p(x=5).
-From b above, we already have p(x=2)=0.2107. Therefore:
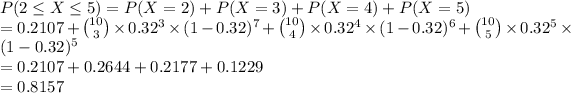
-Hence the probability of between two and five is 0.8157