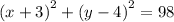Answer:
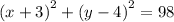
Explanation:
The standard form equation of a circle is given as:

Where (a,b) is the center and r is the radius.
We need to use the distance formula to obtain the radius.
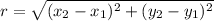
We substitute the center (-3,5) and (4,-2) to get:

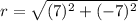
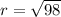
We now substitute the center and radius to get:
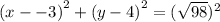
The standard form equation is;