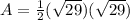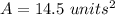Question

In △ABC,∠B is a right angle. The coordinates for each point are A(10, 7), B(5, 9), and C(3, 4). ​ Rounded to the nearest tenth, what is the area, in square units, of △ABC ? ​Enter the area in the box.

Answer 1

`A=14.5\ units^2`

Explanation:

we know that

The area of the right triangle ABC is equal to

`A=(1)/(2)(AB)(BC)`

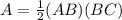
the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

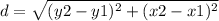
we have

A(10, 7), B(5, 9), and C(3, 4)

step 1

Find the distance AB

A(10, 7), B(5, 9)

substitute in the formula

`d=\sqrt{(9-7)^(2)+(5-10)^(2)}`

`d=\sqrt{(2)^(2)+(-5)^(2)}`

`d_A_B=√(29)\ unjts`

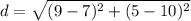
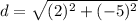
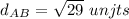
step 2

Find the distance BC

B(5, 9),C(3, 4)

substitute in the formula

`d=\sqrt{(4-9)^(2)+(3-5)^(2)}`

`d=\sqrt{(-5)^(2)+(-2)^(2)}`

`d_B_C=√(29)\ unjts`

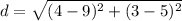
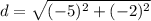
step 3

Find the area

substitute the values

`A=(1)/(2)(√(29))(√(29))`

`A=14.5\ units^2`