Answer:
See explanation
Explanation:
Q1-5.
1. Plane parallel to WXT is ZYU.
2. Segments parallel to
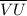 are
are
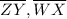 and
and
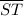
3. Segments parallel to
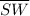 are
are
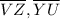 and
and

4. Segments skew to

 are
are
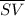 and
and
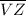 (not lie in the same plane and not parallel)
(not lie in the same plane and not parallel)
5. Segments skew to

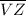 are
are
 and
and
 (not lie in the same plane and not parallel)
(not lie in the same plane and not parallel)
Q6.
a.
 and
and
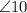 are the same-side interior angles, transversal k
are the same-side interior angles, transversal k
b.
 and
and
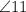 are alternate exterior angles, transversal m
are alternate exterior angles, transversal m
c.
 and
and
 do not form any pair of angles
do not form any pair of angles
d.
 and
and
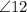 are the same-side exterior angles, transversal k
are the same-side exterior angles, transversal k
e.
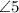 and
and
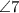 are corresponding angles, transversal j
are corresponding angles, transversal j
f.
 and
and
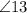 are alternate interior angles, transversal l
are alternate interior angles, transversal l
Q7.
 (as vertical angle with angle 7)
(as vertical angle with angle 7)
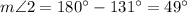 (as supplementary angle with angle 1)
(as supplementary angle with angle 1)
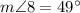 (as vertical angle with angle 2)
(as vertical angle with angle 2)
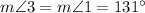 (as corresponding angles when parallel lines p and q are cut by transversal r)
(as corresponding angles when parallel lines p and q are cut by transversal r)
 (as corresponding angles when parallel lines p and q are cut by transversal r)
(as corresponding angles when parallel lines p and q are cut by transversal r)
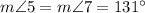 (as corresponding angles when parallel lines p and q are cut by transversal r)
(as corresponding angles when parallel lines p and q are cut by transversal r)
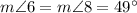 (as corresponding angles when parallel lines p and q are cut by transversal r)
(as corresponding angles when parallel lines p and q are cut by transversal r)
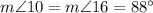 (as vertical angle with angle 16)
(as vertical angle with angle 16)
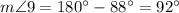 (as supplementary angle with angle 16)
(as supplementary angle with angle 16)
 (as vertical angle with angle 9)
(as vertical angle with angle 9)
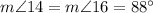 (as corresponding angles when parallel lines p and q are cut by transversal s)
(as corresponding angles when parallel lines p and q are cut by transversal s)
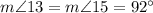 (as corresponding angles when parallel lines p and q are cut by transversal s)
(as corresponding angles when parallel lines p and q are cut by transversal s)
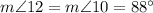 (as corresponding angles when parallel lines p and q are cut by transversal s)
(as corresponding angles when parallel lines p and q are cut by transversal s)
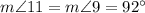 (as corresponding angles when parallel lines p and q are cut by transversal s)
(as corresponding angles when parallel lines p and q are cut by transversal s)
Q8.
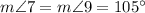 (as vertical angles)
(as vertical angles)
 (as supplementary angle with angle 9)
(as supplementary angle with angle 9)
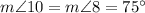 (as vertical angles)
(as vertical angles)
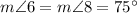 (as alternate interior angles when parallel lines a and b are cut by transversal c)
(as alternate interior angles when parallel lines a and b are cut by transversal c)
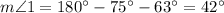 (by angle addition postulate)
(by angle addition postulate)
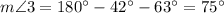 (by angle addition postulate)
(by angle addition postulate)
 (as vertical angles)
(as vertical angles)
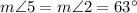 (as vertical angles)
(as vertical angles)
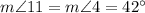 (as alternate interior angles when parallel lines a and b are cut by transversal d)
(as alternate interior angles when parallel lines a and b are cut by transversal d)
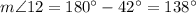 (as supplementary angles)
(as supplementary angles)
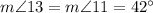 (as vertical angles)
(as vertical angles)
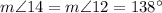 (as vertical angles)
(as vertical angles)