Question

The parent function of the function represented in the table is

quadratic, linear ,exponential
If function f was translated down 4 units, the
f(x),x, x- and f(x)
-values would be
multiplied by 4 , increased by 4 ,decreased by 4 , divided by 4
A point in the table for the transformed function would be
(4,87) ,(3,29) ,(2,23) ,(1,52)

Answer 1

`y=3^x+10`

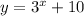
f(x)-values

decreased by 4

(4,87)

Explanation:

The table shows the exponential growth function

`y=a\cdot b^x +c`

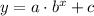
substitute some values to find
`a,b,c:`

`13=a\cdot b^1+c\\ \\19=a\cdot b^2 +c\\ \\37=a\cdot b^3+c`

Subtract these equations:

`ab^2+c-ab-c=19-13\Rightarrow ab(b-1)=6\\ \\ab^3+c-ab^2-c=37-19\Rightarrow ab^2(b-1)=18`

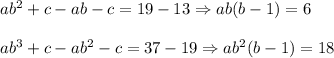
Divide them:

`(ab^2(b-1))/(ab(b-1))=(18)/(6)\Rightarrow b=3`

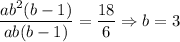
Then

`3a(3-1)=6\Rightarrow a=1`

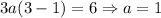
Hence,

`13=1\cdot 3+c\Rightarrow c=10`

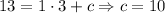
Therefore, the parent function is
`y=3^x+10`

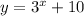
If this function would be translated 4 units down, its expression will be

`y=3^x+10-4\\ \\y=3^x+6`

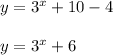
This means that f(x)-values decreased by 4.

Then the table for translated function is

`\begin{array}{cccccc}x&1&2&3&4&5\\ \\f(x)&9&15&33&87&249\end{array}`

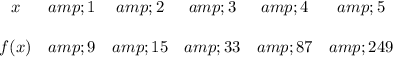
The graph of translated function passes through the point (4,87)

Answer 2

1. Exponential

2. F(x)

3. Decreased by 4

4. (4,87)

Explanation: