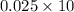Answer:
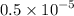 ,
,
0.00025,
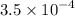 ,
,
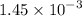 ,
,
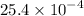 ,
,
0.025,
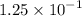 ,
,
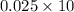
Explanation:
We can do it this way.
First, let us clear off the powers by multipying each number by
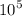
This implies that,
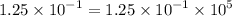
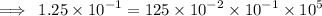
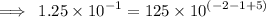
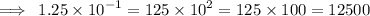
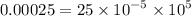
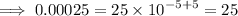
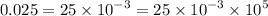
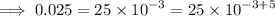
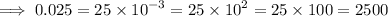

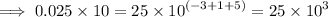
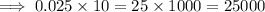
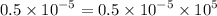
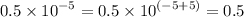

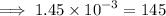

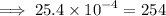
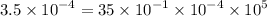
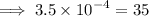
Arranging in order from the smallest, we have;
0.5,25,35,145,254,2500,12500,25000
Hence,
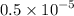 ,
,
0.00025,
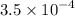 ,
,
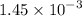 ,
,
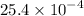 ,
,
0.025,
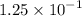 ,
,