Question

The flight of a kicked football follows the quadratic function f(x)=−0.02x^2+2.2x+2, where f(x) is the vertical distance in feet and x is the horizontal distance the ball travels. How far, in feet, will the ball travel across the field by the time it hits the ground? Round your answer to one decimal place.

Answer 1

110.9

Explanation:

The highest point is the y-value of the turning point. Thus we need to find the maximum quadratic function

showing that the ball will reach a maximum height of 72.5 feet.

Answer 2

110.9 feet

Explanation:

The function that models the flight of the ball is

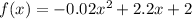`f(x) = - 0.02 {x}^(2) + 2.2x + 2`where f(x) is the vertical distance in feet and x is the horizontal distance the ball travels

If the ball hits the ground, then f(x)=0

`\implies - 0.02 {x}^(2) + 2.2x + 2 = 0`

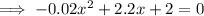
The solution is given by the quadratic formula:

`x = \frac{ - b \pm \sqrt{ {b}^(2) - 4ac} }{2a}`

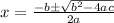
We substitute a=-0.02, b=2.2, and c=2 to get:

`x = \frac{ - 2.2 \pm \sqrt{ {2.2}^(2) - 4 * - 0.02 * 2} }{2 * - 0.02}`

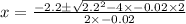
This implies that:

`x = 110.90 \: or \: x = - 0.90`

Since we are dealing with time,

`x = 110.90`

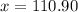
To one decimal place, we have 110.9 feet