Question

Find the 51st term of the arithmetic sequence 25, 12, -1, ...

Answer 1

Explanation:

The formula for determining the nth term of an arithmetic sequence is expressed as

Tn = a + d(n - 1)

Where

a represents the first term of the sequence.

d represents the common difference.

n represents the number of terms in the sequence.

From the information given,

a = 25

d = 12 - 25 = - 1 - 12 = - 13

n = 51

We want to determine the value of the 51st term, T51. Therefore,

T51 = 25 - 13(51 - 1)

T51 = 25 - 650

T51 = - 625

Answer 2

Answer: -625

Step-by-step explanation: The first thing we want to do is determine if this sequence is an arithmetic sequence. So we want to look at the terms and ask ourselves is the difference between the terms exactly the same. In this case, the difference between terms is 13 which means that we have an arithmetic sequence.

To determine the 51st term, you could keep on subtracting 51 all the way until you get to the 51st term. However, if you're taking a test, that's probably not the best use of your time so we want to be efficient.

So what we are going to use to calculate the 51st term in this arithmetic sequence is our explicit formula which is shown below.

`^(a)n = ^(a)1 + (n - 1) d`

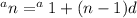
In the formula above, n is how many terms we are solving for which in this case is 51 terms so we can plug 51 in for n in the formula.

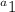`^(a)1` will be the first term in the sequence which is 25.

Then d is the common difference which is -13.

Now we have all our information but we need to substitute these values into our explicit formula to find our answer.

So we have
`^(a) 51 = 25 + (51 - 1)(-13)`.

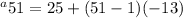Now, make sure we apply order of operations because this is where many students make mistakes. Remember to simplify inside the parentheses first.

(51 - 1) is going to be 50.

So we have ^{a} 51 = 25 + (50)(-13).

Then, we have to make sure we multiply before we add.

So (50)(-13) is going to be -650.

So we have ^{a} 51 = 25 + (-650) which is -625.