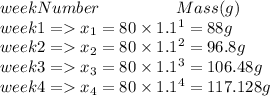Answer:
a.
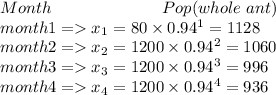
b.
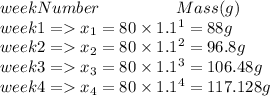
Explanation:
a. From the information provided, we can deduce that the population death's follows a Geometric sequence in the form
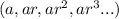 where
where
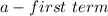 and
and
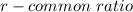
#Since the population is reducing,
 can is obtained as
can is obtained as
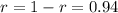
#The
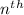 term is obtained using the formula
term is obtained using the formula
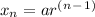 , given a=1200
, given a=1200
The number of ants alive after every month (in first 4 months)
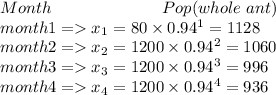
The ant's alive after 4 months is obtained as the value of
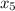
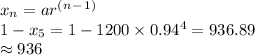
Hence, 936 ants are alive after 4 months.
b. As with the above question, the kitten population follows a geometric sequence:
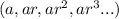 .
.
#Since it's a growing population , the common ration is the sum of 100% + the growth rate,
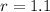 and
and
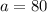 and
and
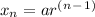
The population after 4weeks will be: