Your question is incomplete. The complete question is attached down
Answer:
JM = 20 units
Explanation:
∵ Hexagon RSTUVW is similar to hexagon JKLMNP
∴ The corresponding sides and diagonals have a constant ratio
∴
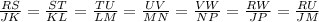
∵ ST = 6 units
∵ KL = 10
∴
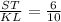
- Simplify it by dividing up and down by 2
∴
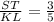
∵
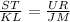
∵ RU = 12 units
∴
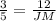
- By using cross multiplication
∴ JM × 3 = 5 × 12
∴ 3 JM = 60
- Divide both sides by 3
∴ JM = 20 units