Answer:
Barbara's speed in clear weather is
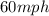 and in the thunderstorm is
and in the thunderstorm is
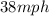 .
.
Explanation:
Let
 be the speed and
be the speed and
 be the time Barbara drives in clear weather, and let
be the time Barbara drives in clear weather, and let
 be the speed and
be the speed and
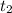 be the time she drives in the thunderstorm.
be the time she drives in the thunderstorm.
Barbara drives 22 mph lower in the thunderstorm than in the clear weather; therefore,
(1).
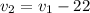
Also,
(2).
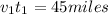
(3).
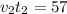 ,
,
and
(4).
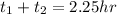
From equations (2) and (3) we get:

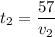
putting these in equation (4) we get:
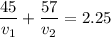
and substituting for
 from equation (1) we get:
from equation (1) we get:
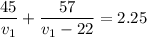
This equation can be rewritten as
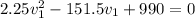
which has solutions
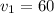

We take the first solution
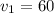 because it gives a positive value for
because it gives a positive value for
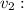
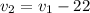
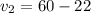
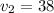 .
.
Thus, Barbara's speed in clear weather is
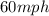 and in the thunderstorm is
and in the thunderstorm is
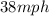 .
.