The lengths are AB 2
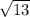 cm, BC
cm, BC
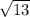 cm, CD 2
cm, CD 2
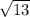 cm and DA
cm and DA
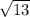 cm
cm
Explanation:
Given,
The vertices of quadrilateral are A(1,-1), B(-5,3), C(-3,6) and D(3,2)
To find the lengths of the sides of ABCD
Formula
The length of two points (x1,y1) and (x2,y2) is
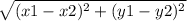
So,
AB ⇒
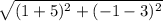 cm =
cm =
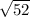 cm = 2
cm = 2
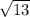 cm
cm
BC ⇒
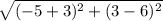 cm =
cm =
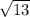 cm
cm
CD ⇒
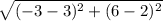 cm =
cm =
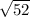 cm = 2
cm = 2
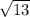 cm
cm
DA ⇒
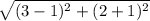 cm =
cm =
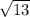 cm
cm