Question

A 0.311 kg tennis racket moving 30.3 m/s east makes an elastic collision with a 0.0570 kg ball moving 19.2 m/s west. Find the velocity of the tennis racket after the collision.

Answer 1

The velocity of tennis racket after collision is 14.96m/s

Step-by-step explanation:

Given-

Mass, m = 0.311kg

u1 = 30.3m/s

m2 = 0.057kg

u2 = 19.2m/s

Since m2 is moving in opposite direction, u2 = -19.2m/s

Velocity of m1 after collision = ?

Let the velocity of m1 after collision be v

After collision the momentum is conserved.

Therefore,

m1u1 - m2u2 = m1v1 + m2v2

`v1 = ((m1-m2)/(m1+m2))u1 + ((2m2)/(m1+m2))u2`

`v1 = ((0.311-0.057)/(0.311+0.057))30.3 + ((2 X 0.057)/(0.311 + 0.057)) X-19.2\\\\v1 = ((0.254)/(0.368) )30.3 + ((0.114)/(0.368)) X -19.2\\ \\v1 = 20.91 - 5.95\\\\v1 = 14.96`

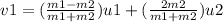
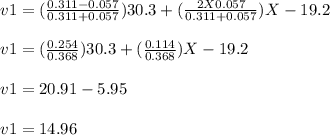
Therefore, the velocity of tennis racket after collision is 14.96m/s