The velocity at mean position is 50 cm/sec
Step-by-step explanation:
The spring is stretched by a force = 200 x 980 dynes through a length 100 cm . By Hooks law The force F = - k x
here k is spring constant and x is displacement of weight .
Thus 200 x 980 = - k x 100
or k = 1960 dynes/cm
The time period of spring can be found by relation
T = 2π
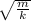
= 2π
 = 2 sec
= 2 sec
The frequency of vibration is taken as the reciprocal of time period
Thus frequency ν =
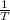 =
=
 = 0.5 revolution / sec
= 0.5 revolution / sec
b. The maximum acceleration is at the end points of vibration , and is equal to acceleration due to gravity .
c. The velocity at mean position can be calculated from the kinetic energy relation of spring .
The kinetic energy of spring =
 k x²
k x²
and it is converted into kinetic energy of mass at mean position
Thus
 k x² =
k x² =
 m v²
m v²
or v =
 x
x
=
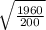 x 5 = 50 cm/sec
x 5 = 50 cm/sec