The other two vertices are (7, 5) and (8, -1)
Explanation:
Given,
Two vertices of a parallelogram are A(1,1) and B(0,7)
The diagonals meet at (4,3)
To find the other two vertices of the parallelogram.
We know that the diagonals of a parallelogram intersect each other.
Let, C be the vertex as (x,y)
According to the problem
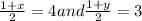
or, 1+x = 8 and 1+y = 6
or, x = 7 and y = 5
Again, let D be the vertex as (a,b)
According to the problem,

or, a = 8 and 7+b = 6
or, a= 8 and b= -1
Hence the vertices are (7, 5) and (8, -1)