Question

There are three parts to number and there is a number 2. Complete all

questions.
Daisha is sitting on the bus on the way home from school and is thinking
about the fact that she has three homework assignments to do tonight. The
table below shows her estimated probabilities of completing 0, 1, 2, or all 3
of the assignments.
Number of Homework Assignments Completed
0
3
Probability
Writing your answers as fractions in lowest terms, find the probability that
Daisha completes:
a. Exactly one assignment
b. More than one assignment
c. At least one assignment
2. Find the probability that the number of homework assignments Daisha​

Answer 1

a. 2/9

b. 11/18

c. 5/6

d. 13/18

Step-by-step explanation:

Answer 2

• a. 2/9

• b. 11/18

• c. 5/6

• d. 13/18

Step-by-step explanation:

The question is incomplete. It is missing the probability table.

A similar question in the internet has this table

Number of Homework Assignments Completed 0 1 2 3

Probability 1/6 2/9 5/18 1/3

Also the question #2 is incomplete. You can complete it with: "Find the probability that the number of homework assignments Daisha​ completes is not exactly 2"

Solution

a. Probability that Daisha completes: Exactly one assignment

For this you must understant what a the table represents. It is a table of a discrete random variable. The random variable is the number of homework assignments completed. The probability table gives the probability for each one of the possible values of the random variable.

This is, you have:

• P(X=0) = 1/6
• P(X=1) = 2/9
• P(X=2) = 5/18
• P(X=3) = 1/3

That lists all the possible values of the random variable each with its corresponding probability. Thus, those probabilities must add up 1. Check it:

`(1)/(6)+(2)/(9)+(5)/(18)+(1)/(3)=(3+4+5+6)/(18)=(18)/(18)=1\checkmark`

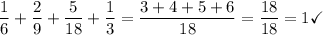
Note that the events are all mutually exclusive of the others: every probability is the probability that the random variable takes exactly that value. I mean, 1/6 is the probability of completing exactly none homework assignment, 2/9 is the probability of completing exactly one homework assigment, and so on.

Then, the asnwer to the first question, is that the probability that Daisha completes: exactly one assignment is 2/9.

b. Probability that Daisha completes: More than one assignment

The probability that Daisha completes more than one assignment is the probability that she completes 2 or 3 assignments.

Using the corresponding notation for discrete random variables, and the fact that they are mutually exclusive events, that is:

• P(X > 1) = P(X = 2) + P(X = 3)

From the table:

• P(X = 2) = 5/18
• P(X = 3) = 1/3

`P(X>1)=(5)/(18)+(1)/(3)=(5+6)/(18)=(11)/(18)`

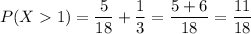
Thus the answer is 11/18

c. Probability that Daisha completes: At least one assignment

The probability that Daisha completes at least one assignment is the complete to that she completes none assignment, this is:

• P(X ≥ 1) = 1 - P(X = 0)

`P(X\geq 1)=1-P(X=0)=1-(1)/(6)=(5)/(6)`

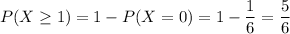
Note that that is the same as:

`P(X\geq 1)=P(X=1)+P(X=2)+P(X=3)=\\\\\\=(2)/(9)+(5)/(18)+(1)/(3)=(4+5+6)/(18)=(15)/(18)=(5)/(6)`

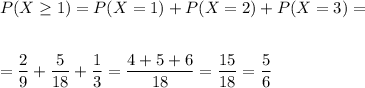
2. Find the probability that the number of homework assignments Daisha​ completes is not exactly 2.

The probability that the number of assignments Daisha completes is not exactly 2, is that it is 0, 1, or 3.

Mathematically:

`P(X\\eq2)=1-P(X=2)\\\\\\P(X\\eq2)=1-(5)/(18)=(18-5)/(18)=(13)/(18)`

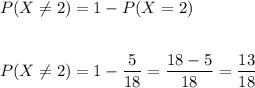
You can verify that that is the same as: P(X=0) + P(X=1) + P(X=3).

Therefore, the answer is 13/18