Answer:
The vertex of the graph is (-3 , -2)
Explanation:
The quadratic equation y = ax² + bx + c is represented graphically by a parabola
The parabola has a vertex point (h , k) which is divided it into two congruent parts
- The equation of the axis of symmetry of the parabola is x = h
- The minimum/maximum value of the equation is at y = k
You can find the vertex algebraically by using the rule h =
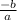 and k is the value of y at x = h
and k is the value of y at x = h
You can find it graphically by write the coordinates of the lowest or greatest point in the graph of the parabola
From the attached figure
∵ The parabola is opened up-ward
∵ It has a lowest point at x = -3 and y = -2
∵ The coordinates of the vertex of the parabola are (h , k)
∵ The vertex of the parabola is the lowest point
∴ h = -3 and k = -2
∴ The vertex of the parabola is (-3 , -2)
The vertex of the graph is (-3 , -2)