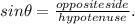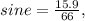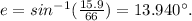Question

Please help me and can you show full working

Answer 1

1. a = 491.49 cm,

2. b = 2.875 m,

3. c = 130.737 m,

4. d = 30.464°, and

5. e = 13.940 ° (sixth figure not visible).

Explanation:

Step 1:

The three basic formula needed to solve these questions are:

`sin\theta = (oppositeside)/(hypotenuse) , cos\theta = (adjacentside)/(hypotenuse), tan\theta= (opposite side)/(adjacent side).`

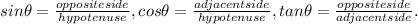
To calculate, the angles we use

`\theta = sin^(-1) ((oppositeside)/(hypotenuse)) , \theta = cos^(-1) ((adjacentside)/(hypotenuse)), \theta= tan^(-1) ((opposite side)/(adjacent side)).`

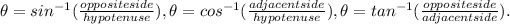
Step 2:

The triangle's angle = 85°, opposite side = a cm and adjacent side = 43 cm. So

`tan\theta= (opposite side)/(adjacent side).`
`tan85= (a)/(43).`,
`a = 11.430 (43) = 491.49 cm,`

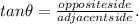
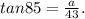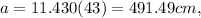
Step 3:

The triangle's angle = 49°, opposite side = b m and adjacent side = 2.5 m. So

`tan\theta= (opposite side)/(adjacent side).`
`tan49= (b)/(2.5),`
`b = 1.150 (2.5) = 2.875 m.`

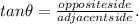
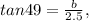
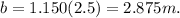
Step 4:

The triangle's angle = 44°, hypotenuse = c m and adjacent side = 94 m. So

`cos\theta= (adjacent side)/(hypotenuse).`
`cos44= (94)/(c),`
`c = (94)/(0.719) = 130.737 m.`

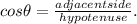
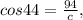
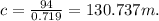
Step 5:

The triangle's angle = d°, opposite side = 1.8 m and hypotenuse = 35 cm = 3.55 m.

`sin\theta= (opposite side)/(hypotenuse).`
`sin d= (1.8)/(3.55),`
`d = sin^(-1) ((1.8)/(3.55)) = 30.464^(\circ).`

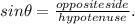
Step 6:

The triangle's angle = e°, opposite side = 15.9 m and hypotenuse = 66 cm = 3.55 m.

`sin\theta= (opposite side)/(hypotenuse).`
`sin e= (15.9)/(66),`
`e = sin^(-1) ((15.9)/(66)) = 13.940^(\circ).`