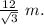Answer:
The base of triangle is
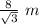 and the height of triangle is
and the height of triangle is
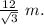
Explanation:
Given:
A triangle has a base of x 1/2 m and a height of x 3/4 m. If the area of the triangle is 16m to the power of 2.
Now, to find the base and height of the triangle.
The base of triangle =
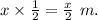
The height of triangle =
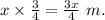
The area of triangle =
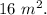
Now, we put the formula of area to solve:
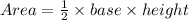

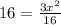
Multiplying both sides by 16 we get:

Dividing both sides by 3 we get:
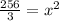
Using square root on both sides we get:
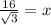
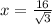
Now, by substituting the value of
 to get the base and height:
to get the base and height:
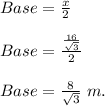
So, the base of triangle =
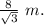
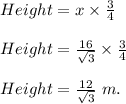
Thus, the height of triangle =
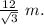
Therefore, the base of triangle is
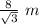 and the height of triangle is
and the height of triangle is