Question

Elentine started with 110 lirts on his farm. Every hour he exploded 4 more of them. Farmer Hab started with 33 lirts oh her farm every hour she bought 7 more of them.

Write a system of equations in slope intercept form to model each farmers lirts (y) as hours (x) increase

Answer 1

The system of equations in the slope-intercept form is;

Farmer Elentine:
`y = - 4x + 110`.

Farmer Hab:
`y =7x + 33`.

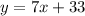Explanation:

Step 1:

Farmer Elentine starts with 110 lirts on his farm. So the constant for the equation is 110. If he explodes 4 of them with every passing hour

after 1 hour, lirts exploded =
`4(1) = 4`,

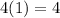after 2 hours, lirts exploded =
`4(2) = 8`,

after x hours, lirts exploded =
`4(x) = 4x`.

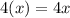Step 2:

To calculate the lirts in a particular period of time, we subtract the number of lirts exploded from 110.

The slope-intercept form is
`y = mx +b.`

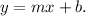
If y represents the number of lirts and x is the number of hours, then

`y = - 4x + 110`.

Step 3:

Farmer Hab started with 33 lirts on her farm. So the constant for the equation is 33. If she bought 7 of them with every passing hour,

after 1 hour, lirts bought =
`7(1) = 7`,

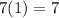after 2 hours, lirts bought =
`7(2) = 14`,

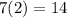after x hours, lirts bought =
`7(x) = 7x`.

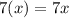Step 4:

To calculate the lirts in a particular period of time, we add the number of lirts bought with 33.

The slope-intercept form is
`y = mx +b.`

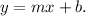
If y represents the number of lirts and x is the number of hours, then

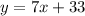`y =7x + 33`.