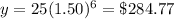Question

There is a hot market at school for used graduation gowns, in fact, the price is growing exponentially! Last week!

could have gotten one for $25, but today, one week later, the price is $37.50. What would the price be if I decide
to wait to buy my graduation gown at graduation, six weeks from now? Show your work.

Answer 1

`\$284.77`

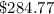
Explanation:

we know that

The equation of a exponential growth function is equal to

`y=a(1+r)^x`

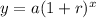
where

y is the price in dollars

x is the number of weeks

a is the initial value

r is the rate of change

we have

`a=\$25`

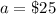
substitute

`y=25(1+r)^x`

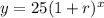
Remember that

one week later, the price is $37.50

so

we have the ordered pair (1,37.50)

substitute in the exponential function

`37.50=25(1+r)^1`

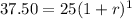
solve for x

`37.50=25(1+r)\\r=(37.50/25)-1\\r=0.5`

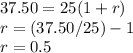
substitute

`y=25(1+0.50)^x`

`y=25(1.50)^x`

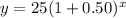
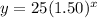
For x=6 weeks

substitute the value of x

`y=25(1.50)^6=\$284.77`