Question

Which of these systems of equations has no solution? Select three that apply. 14x + 7y = 30 14x + 7y = 40 17x – 10y = 38 17x –12y = 38 7x – 15y = 26 8x – 15y = 26 18x + 5y = –42 19x + 6y = –44 11x – 2y = –25 11x – 2y = –20 5x + 9y = 34 5x + 9y = 27

Answer 1

Explanation:

We are given a system of equations and have to find out which do not have solution

`i) 14x + 7y = 30\\ 14x + 7y = 40`

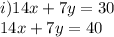
these two are parallel lines and hence will never intersect. So no solution

`ii) 17x - 10y = 38\\ 17x -12y = 38`

Subtracting we get y =0 and x =38/17 hence solution exist.

`iii) 7x -15y = 26 \\8x - 15y = 26`

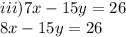
Subtract to get x =0 and y = -26/15. Hence solution exist.

iv)
`18x + 5y = -42\\ 19x + 6y = -44`

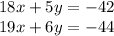
these two are non parallel hence intersection so solution is there.

`11x - 2y = -25\\ 11x -2y = -20`

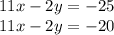
these two are parallel lines and hence no solution

`5x + 9y = 34 \\5x + 9y = 27`

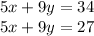
these two are parallel lines and hence no solution