Question

7. What is the system of equations that describes the following graph?

Answer 1

The system of equations that describes the graph is:

x + y = 3

2x + 2y = 1

Explanation:

Parallel lines have:

• Same slopes
• Different y-intercepts
• The system of equations which represent them is y = m x + b and y = m x + c, where b and c are the y-intercepts

Let us find the equation of each line

∵ The solid line passes through points (3 , 0) and (0 , 3)

∵ m = Δy/Δx

∴ Δy/Δx =
`(3-0)/(0-3)=(3)/(-3)`

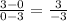
∴ m = -1

∵ b is the y-intercept (value y at x = 0)

∵ y = 3 at x = 0

∴ b = 3

∴ y = - x + 3

- Add x to both sides

∴ x + y = 3 ⇒ (1)

∵ The dashed line passes through points (0.5 , 0) and (0 , 0.5)

∵ m = Δy/Δx

∴ Δy/Δx =
`(0.5-0)/(0-0.5)=(0.5)/(-0.5)`

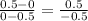
∴ m = -1

∵ b is the y-intercept (value y at x = 0)

∵ y = 0.5 at x = 0

∴ b = 0.5

∴ The equation of the line is y = - x + 0.5

- Add x to both sides

∴ x + y = 0.5

- Multiply both sides by 2

∴ 2x + 2y = 1 ⇒ (2)

The system of equations that describes the graph is:

x + y = 3

2x + 2y = 1