Question

A 14 gram sample of a substance thats used to sterilize surgical instruments has a k-value of 0.1481. find the substance half-life, in days round answer to the nearest tenth

Answer 1

4.7

Explanation:

I got 100% on my test.

Answer 2

The half life of the substance is
`\tau = 4.7 \:days`.

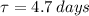Explanation:

The equation that models the amount of substance after time
`t` is

`A = A _0 e^(-kt)`.

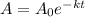We are told that that the initial amount
`A_0= 14g`, and the k-value is
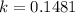`k = 0.1481`; therefore,

`A = 14e^(-0.1481t)`

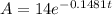
The half-life of the substance is the amount of time
`\tau` it takes to decay to half its initial value; therefore,

`(A_0)/(2) = A_0e^(-0.1481\tau )`

`e^(-0.1481\tau ) = (1)/(2).`

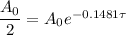
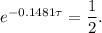
Take the Natural Logarithm of both sides and get:

`ln[e^(-0.1481\tau ) ]= ln[(1)/(2)]`

`-0.1481\tau = ln[(1)/(2) ]`

`\tau = (ln[(1)/(2) ])/(-0.1481)`

`\boxed{\tau = 4.7 \:days}`

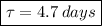
Thus, we find that the half life of the substance is 4.7 days.