It will cost 2,464 currency for plastering 448
 of the wall.
of the wall.
Explanation:
Step 1:
The volume of this room is determined by multiplying its length, breadth, and height.
From the question;
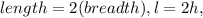
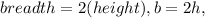
So
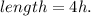
Step 2:
The volume of the room
 ,
,
Substituting the values of length and breadth in the above equation, we get
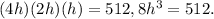
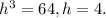
So

So l = 16 m, w = 8 m and h = 4 m.
Step 3:
If each
 of the wall costs 5.50, we need to calculate the surface area of the room.
of the wall costs 5.50, we need to calculate the surface area of the room.
There are six sides of the room (2 sets of 3 sides)
Area of the
 set =
set =

Area of the
 set =
set =
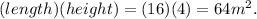
Area of the
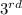 set =
set =
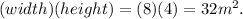
The Surface area of these three sets = 128 + 64 + 32 = 224
 .
.
Since there are two sets,
The total surface area =
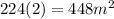 .
.
Step 4:
If each
 of the wall costs 5.50,
of the wall costs 5.50,
448
 costs;
costs;
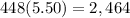 currency.
currency.