Question

Which set of data has the highest interquartile range?

Answer 1

See explanation

Explanation:

You have not provided enough information to get a unique answer.

But I will show you how to calculate the interquartile range from the boxplots and compare them.

From the first diagram, the first quartile is

`Q_1=3.5`

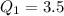
and the 3rd quartile is

`Q_3=8.5`

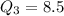
The interquartile range is

`IQR=Q_3-Q_1 = 8.5 - 3.5`

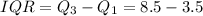
Similarly from the second diagram,

`IQR=Q_3-Q_1 = 9.5 - 5 = 4.5`

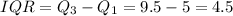
Therefore the first has the highest interquartile range.