Question

For every mile of highway on land, the city needs two truckloads of asphalt and one gallon of paint. For every mile of highway on bridges, the city needs one truckload of asphalt and three gallons of paint. The city has 50 truckloads of asphalt and 80 gallons of paint. A. What is the largest total number of miles of highway the city can build? B. Suppose the city is on an island and must build at least 25 miles of highway on bridges to reach other islands. Now what is the largest total number of miles of highway the city can build?

Answer 1

A. 36 miles

B. 30 miles

Explanation:

Let x miles be the number of miles of highway and y miles be the number of miles of highway on bridges the city can build.

Part A:

For every mile of highway on land, the city needs two truckloads of asphalt and one gallon of paint, so for x miles the city needs 2x truckloads of asphalt and x gallons of paint.

For every mile of highway on bridges, the city needs one truckload of asphalt and three gallons of paint, so for y miles the city needs y trackloads of asphalt and 3y gallons of paint.

The city has 50 truckloads of asphalt, thus

`2x+y\le50`

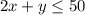
The city has 80 gallons of paint, so

`x+3y\le80`

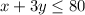
You get the system of two inequalities:

`\left\{\begin{array}{l}2x+y\le 50\\ \\x+3y\le 80\end{array}\right.`

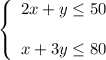
Plot the solution region on the coordinate plane (see first attached diagram).

The total number of miles is
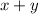`x+y`. Its maximum value is at intersection point of lines
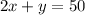`2x+y=50` and
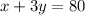`x+3y=80`. Find the coordinates of this point:

`y=50-2x\\ \\x+3(50-2x)=80\\ \\x+150-6x=80\\ \\-5x=-70\\ \\x=14\\ \\y=22\\ \\x+y=36`

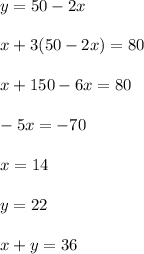
Part B:

Suppose the city is on an island and must build at least 25 miles of highway on bridges, then the city needs

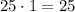`25\cdot 1=25` trackloads of asphalt

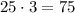`25\cdot 3=75` gallons of paint

Then

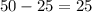`50-25=25` trackloads of asphalt and

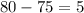`80-75=5` gallons of paint are left.

Hence,

`2x+y\le 25\\ \\x+3y\le 5`

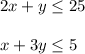
Plot the solution region on the coordinate plane (see second attached diagram). The total number of miles is
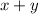`x+y`. Its maximum value is at point (5,0), hence
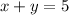`x+y=5` and the total number of miles is

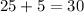`25+5=30` miles.