Question

If we toss a fair coin until we get two consecutive heads or two consecutive tails, let X be the number of tosses. If you toss a fair coin until you get a tail that is preceded by a head, let Y be the number of tosses. (1). Find the PMF of X and E(X). (2). Find the PMF of Y and E[Y].

Answer 1

1) PMF of X and E(X) is 3

2) PMF of Y and E[Y] is 4

Explanation:

(1). Find the PMF of X and E(X)

it has to have TT and HH at end

if at end there is TT then the sequence has to be : .......THTHTHTT

if at end there is HH then the sequence has to be : .......HTHTHTHH

no. of tosses before last two = x-2

these x-2 tosses also have fix pattern so,

P(......TT) =
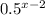`0.5^(x-2)` x P(TT)

=
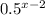`0.5^(x-2)` x (0.5 x 0.5) =
`0.5^(x)`

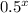
P(TT at the end of X tosses) =
`0.5^(x)`

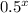
similarly,

P(HH at the end of X tosses) =
`0.5^(x)`

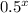
P(X) = P(TT at the end of X tosses) + P(HH at the end of X tosses)

P(X) = 2 x (
`0.5^(x)` )

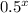E(X) = Σx.2*(
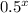`0.5^(x)` ) {x >= 2}

E(X) = 3

2. Find the PMF of Y and E[Y].

For the y-2 tosses before the HT if there is any heads then it will only be succeeded by heads till we reach the HT

therefore the y-2 tosses before HT are of the form : TkH(y-2)-k

k can be 0 to y-2 therfore y-2 +1 possibilities

k can have y-1 values

P(y) = (y-1)(
`0.5^(y)`)

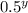E(y) = Σy.(y-1)(
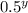`0.5^(y)`) {y >= 2}

E(y) = 4