Question

The mean weight of an adult is 76 kilograms with a variance of 100. If 142 adults are randomly selected, what is the probability that the sample mean would differ from the population mean by more than 1.5 kilograms

Answer 1

7.34% probability that the sample mean would differ from the population mean by more than 1.5 kilograms

Explanation:

To solve this question, we need to understand the normal probability distribution and the central limit theorem.

Normal probability distribution:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Central limit theorem:

The Central Limit Theorem estabilishes that, for a random variable X, with mean
`\mu` and standard deviation
`\sigma`, a large sample size can be approximated to a normal distribution with mean \mu and standard deviation, which is also called standard error
`s = (\sigma)/(√(n))`

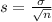
In this problem, we have that:

The standard deviation is the square root of the variance. So

`\mu = 76, \sigma = √(100) = 10, n = 142, s = (10)/(√(142)) = 0.84`

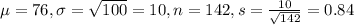
What is the probability that the sample mean would differ from the population mean by more than 1.5 kilograms

Either it will differ by 1.5 or less kilograms, or it will differ by more than 1.5 kilograms. The sum of the probabilities of these events is 100%. I will first find the probability that it differs by 1.5 or less kilograms.

Probability that it differs by 1.5 or less kilograms.

pvalue of Z when X = 76 + 1.5 = 77.5 subtracted by the pvalue of Z when X = 76 - 1.5 = 74.5. So

X = 77.5

`Z = (X - \mu)/(\sigma)`

By the Central Limit Theorem

`Z = (X - \mu)/(s)`

`Z = (77.5 - 76)/(0.84)`

`Z = 1.79`

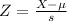
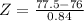
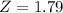
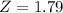`Z = 1.79` has a pvalue of 0.9633

X = 74.5

`Z = (X - \mu)/(s)`

`Z = (74.5 - 76)/(0.84)`

`Z = -1.79`

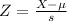
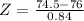
`Z = -1.79` has a pvalue of 0.0367

0.9633 - 0.0367 = 0.9266

92.66% probability that it differs by 1.5 or less kilograms

Probaiblity that it differs by more than 1.5 kilograms

p + 92.66 = 100

p = 7.34

7.34% probability that the sample mean would differ from the population mean by more than 1.5 kilograms