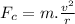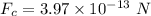Answer:
a)
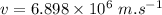 is the speed of each proton
is the speed of each proton
b)
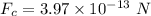
Step-by-step explanation:
Given:
radius of path of motion,
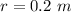
we know charge on protons,

magnetic field strength,
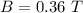
we've mass of proton,

a)
From the equivalence of magnetic force and the centripetal force on the proton:

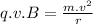
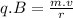
where:
v = speed of the proton
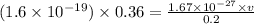
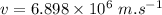 is the speed of each proton
is the speed of each proton
b)
Now the centripetal force on each proton: