Answer:
(a) P (42 ≤ X ≤ 58) = 0.9108
(b) P (X ≥ 50) = 0.5398
Explanation:
The random variable X is defined as the number of heads.
The probability of tossing a Heads in a single flip is, P (X) = p = 0.50.
The coin was flipped n = 100 times.
The random variable thus follows a Binomial distribution with parameters n and p.
As the sample size is too large (n > 30) and the probability of success is closer to 0.50, the binomial distribution can be approximated by the Normal distribution.
The mean of this distribution is:
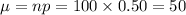 .
.
The standard deviation of this distribution is:
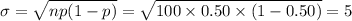
(a)
Compute the value of P (42 ≤ X ≤ 58) by applying the continuity correction as follows:
After applying the continuity correction the probability statement is:
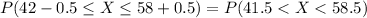
The probability is:
![P(41.5<X< 58.5)=P((41.5-50)/(5)< X< (58.5-50)/(5))\\=P(-1.75<Z<1.7)\\=P(Z<1.7)-P(Z<-1.7)\\=P(Z<1.7)-[1-P(Z<1.7)]\\=2P(Z<1.7)-1\\=(2*0.9554)-1\\=0.9108](https://img.qammunity.org/2021/formulas/mathematics/college/103m405kqigp0vjigpetyqfs9n6oe06t0q.png)
*Use a z-table for the probability value.
Thus, the value of P (42 ≤ X ≤ 58) by applying the continuity correction is 0.9108.
(b)
Compute the value of P (X ≥ 50) by applying the continuity correction as follows:
After applying the continuity correction the probability statement is:
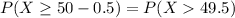
The probability is:
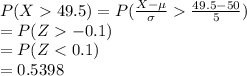
Thus, the value of P (X ≥ 50) by applying the continuity correction is 0.5398.