Question

Your broker has developed a list of firms, their betas, and the return he expects the stock to yield over the next twelve months (labeled "Expected Return"). You have estimated that the risk-free rate is 5% and the return to the market will be 12%. Assuming that CAPM is correct, which stock should you purchase? Firm Beta Expected Return Anderson, Inc. 0.90 10.5% Delta Vanlines 1.24 13.0% Nathan's Bakeries 1.50 16.0% Z-man Electronics 2.15 19.0%

Answer 1

Nathan Bakeries

Step-by-step explanation:

Calculate the required return using the CAPM model in order to compare with the Expected Return and therefore choose the one with the expected return greater than required return

Anderson Inc

RR=5%+0.9(12%-5%)=11.3%

Delta Vanlines

RR=5%+1.24(12%-5%)=13.68%

Nathans Bakeries

RR=5%+1.50(12%-5%)=15.5%

Z-man Electronics

RR=5%+2.15(12%-5%)=20.05%

Therefore the expected return for Nathans Bakeries is greater than the required return so choose Nathans Bakeries.

Answer 2

I would purchase stocks from Nathan's Bakeries which is above their cost of capital according to CAPM

Step-by-step explanation:

We will purchasethe stock based on the CAPM cost of capital to know if the expected return is above or equal to CAPM.

`Ke= r_f + \beta (r_m-r_f)`

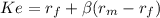
risk free = 0.05

market rate = 0.12

premium market = (market rate - risk free) 0.07

Anderson, Inc.

beta(non diversifiable risk) = 0.9

`Ke= 0.05 + 0.9 (0.07)`

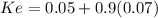
Ke 0.11300 = 11.30%

Expected return 10.5%

NO as it is lower than CAPM

Delta Vanlines

beta(non diversifiable risk) = 1.24

`Ke= 0.05 + 1.24 (0.07)`

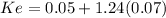
Ke 0.13680 = 13.68%

return 13%

NO as it is lower than CAPM

Nathan's Bakeries

beta(non diversifiable risk) = 1.5

`Ke= 0.05 + 1.5 (0.07)`

Ke 0.15500 = 15.50%

return 16%

YES as it is hihger than CAPM

Z-man Electronics

beta(non diversifiable risk) = 2.15

`Ke= 0.05 + 2.15 (0.07)`

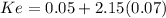
Ke 0.20050 = 20.05%

return 19%

NO as it is lower than CAPM