Question

Calculate the ratio of the kinetic energy of an electron to that of a proton if their wavelengths are equal. Assume that the speeds are nonrelativistic.

Answer 1

`(KE_e)/(KE_p)=1835.16`

Step-by-step explanation:

Given that the wavelengths of electron and proton are equal at non- relativistic speed.

From De-Broglie wave equation we know that:

`\lambda =(h)/(p)`

where:

`\lambda=` wavelength

`h=` Planck's constant

`p=` linear momentum of the particle

Then'

`\lambda_e=\lambda_p`

`(h)/(p_e) =(h)/(p_p)`

`(1)/(m_e.v_e) =(1)/(m_p.v_p)` ..................................(1)

we've mass of electron,
`m_e=9.1* 10^(-31)\ kg`

mass pf proton,
`m_p=1.67* 10^(-27)\ kg`

Now,

kinetic energy of electron:

`KE_e=(1)/(2) m_e.v_e^2`

kinetic energy of proton:

`KE_p=(1)/(2)m_p.v_p^2`

So,

`(KE_e)/(KE_p)=(m_e.v_e^2)/(m_p.v_p^2)`

from eq. (1)

`(KE_e)/(KE_p)=(m_e)/(m_p) * (m_p^2)/(m_e^2)`

`(KE_e)/(KE_p)= (m_p)/(m_e)`

`(KE_e)/(KE_p)=(1.67* 10^(-27))/(9.1* 10^(-31))`

`(KE_e)/(KE_p)=1835.16`

Answer 2

the ratio of the kinetic energy of an electron to that of a proton if their wavelengths are equal is 1835.16 .

Step-by-step explanation:

We know, wavelength is expressed in terms of Kinetic Energy by :

`\lambda=(h)/(√(2mE))`

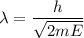
Therefore ,
`E=(h^2)/(2 \lambda^2 m)`

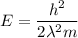
It is given that both electron and proton have same wavelength.

Therefore,

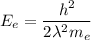`E_e=(h^2)/(2 \lambda^2 m_e)` .... equation 1.

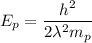`E_p=(h^2)/(2 \lambda^2 m_p)` .... equation 2.

Now, dividing equation 1 by 2 .

We get ,

`(E_e)/(E_p)=((h^2)/(2 \lambda^2 m_e))/((h^2)/(2 \lambda^2 m_p))\\\\\\(E_e)/(E_p)=(m_p)/(m_e)`

Putting value of mass of electron =
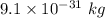`9.1* 10^(-31)\ kg` and mass of proton =
`1.67* 10^(-27)\ kg.`

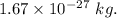
We get :

`(E_e)/(E_p)=(1.67* 10^(-27)\ kg)/(9.1* 10^(-31)\ kg)=1835.16`

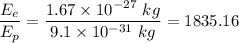
Hence , this is the required solution.