Step-by-step explanation:
Given that,
Refractive index of glass, n₁ = 1.65
Refractive index of liquid, n₂ = 1.22
(a) We need to find the angle of refraction for the angle of incidence of 60°. It can be calculated using Snells law as :
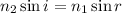
r is the angle of refraction

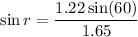
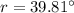
(b)
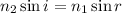
r is the angle of refraction
Here, i = 45 degrees

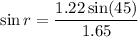
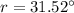
(c)
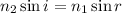
r is the angle of refraction
Here, i = 30 degrees


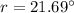
Hence, this is the required solution.