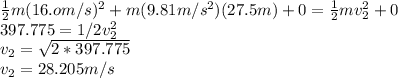Question

A baseball is thrown from the roof of a 27.5 m tall building with an initial velocity of magnitude 16.0m/s and directed at an angle of 37 above the horizontal Using energy methods and ignoring air resistance, calculate the speed of the ball just before it strikes the ground.

Answer 1

Given Information:

distance = y = 27.5 m

Angle = θ = 37°

initial speed of the ball = v1 = 16 m/s

Required Information:

final speed of the ball = v2 = ?

Answer:

v2 = 28.19 m/s

Explanation:

We will write an equation in terms work done by the forces acting on the ball. We know that one force is gravitational force

W = mgy1 - mgy2

kinetic energy is given by

KE = 0.5mv1² so

0.5mv1² + mgy1 = 0.5mv2² + mgy2

Mass cancels out and y2 is zero so equation becomes

0.5v1² + gy1 = 0.5v2²

0.5v2² = 0.5v1² + gy1

v2² = 2*(0.5v1² + gy1)

v2 = √2*(0.5v1² + gy1)

Substitute the values

v2 = √2*(0.5(16)² + 9.8*27.5)

v2 = 28.19 m/s

Therefore, the speed of the ball is 28.19 m/s just before it strikes the ground.

Answer 2

`v_(2)=28.205m/s`

Step-by-step explanation:

Given data

Initial altitude of ball is y₁=27.5m and its initial velocity is v₁=16.0 m/s

We know that,if other forces than gravitational do work,the total work done by all forces is given by:

`W_(tot)=W_(grav)+W_(other)=K_(2)-K_(1)`

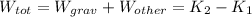
And since the work done is by gravitational force is given by:

Wgrav= -ΔUgrav =mgy₁-mgy₂

And since the kinetic energy is given by:

`K=1/2mv^2`

So we get

`(1)/(2)mv_(1)^2+mgy_(1)+W_(other)=(1)/(2)mv_(2)^2+mgy_(2)`

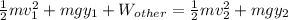
When the ball is thrown there is no other force than the gravitational force which acts on the ball So we have

`W_(other)=0`

Taking the ground to be zero potential energy y₂=0

So we get

`(1)/(2)m(16.om/s)^2+m(9.81m/s^2)(27.5m)+0=(1)/(2)mv_(2)^2+0\\ 397.775=1/2v_(2)^2\\v_(2)=√(2*397.775) \\v_(2)=28.205m/s`