Answer:
The angular displacement of the tub will be 2580.75 rad or 411 revolutions.
Step-by-step explanation:
We know the relation between angular velocity (
 ), the angular displacement (
), the angular displacement (
 ) and time (
) and time (
 ) is given by
) is given by
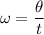
Given
 =
=
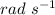 and the time (
and the time (
 ) required to complete a spin is 77.5 s.
) required to complete a spin is 77.5 s.
Therefore, the required angular displacment (
 ) is
) is
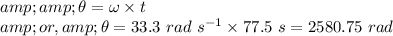
Also we know that,
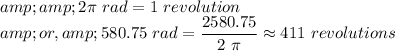
So, the angular displacement of the tub will be 2580.75 rad or 411 revolutions.