Question

A student pushes a 0.2 kg box against a spring causing the spring to compress 0.15 m. When the spring is released, it will launch the box vertically into the air. What is the maximum height the box will reach if the spring constant is 300 N/m?

Answer 1

The maximum height the box will reach is 1.72 m

Step-by-step explanation:

F = k·x

Where

F = Force of the spring

k = The spring constant = 300 N/m

x = Spring compression or stretch = 0.15 m

Therefore the force, F of the spring = 300 N/m×0.15 m = 45 N

Mass of box = 0.2 kg

Work, W, done by the spring =
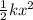`(1)/(2) kx^2` and the kinetic energy gained by the box is given by KE =
`(1)/(2) mv^2`

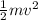
Since work done by the spring = kinetic energy gained by the box we have

`(1)/(2) mv^2` =
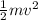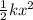`(1)/(2) kx^2` therefore we have v =
`\sqrt{(kx^2)/(m) }` =
`x\sqrt{(k)/(m) }` =
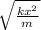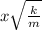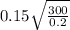`0.15\sqrt{(300)/(0.2) }` = 5.81 m/s

Therefore the maximum height is given by

v² = 2·g·h or h =
`(v^2)/(2g)` =
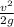`(5.81^(2) )/(2*9.81)` = 1.72 m