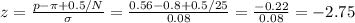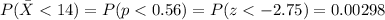Question

An ordinance requiring that a smoke detector be installed in all previously constructed houses has been in effect in a particular city for one year. The fire department is concerned that many houses remain without detectors. Let p = the true proportion of such houses having detectors and suppose that a random sample of 25 homes is inspected. If the sample strongly indicates that fewer than 80% of all houses have a detector, the fire department will campaign for a mandatory inspection program. Because of the costliness of the program, the department prefers not to call for such inspections unless sample evidence strongly argues for their necessity. Let X denote the number of homes with detectors among the 25 sampled. Consider rejecting the claim that p > .8 if x < 15, where x is the observed value of X.

a) what is the probability that the claim is rejected when the actual value of p is .8?
b) what is the probability of not rejecting the claim when the actual value of p is .8?
c) how do the error probabilities of parts (a) and (b) change if the value 15 in the decision rule is replaced by 14?

Answer 1

a. P=0.01222

b. P=0.98778

c. The probability of rejecting the claim is now P=0.00298.

Explanation:

In this case, we evaluate the sampling distribution for a population proportion π=0.8 with a sample size of 25.

We need to calculate the probability of getting a sample mean below 15, which means p=15/25=0.6.

The standard deviation of the sampling distribution is:

`\sigma_M=\sqrt{(\pi(1-\pi))/(N)} =\sqrt{(0.8\cdot0.2)/(25)} =\sqrt{(0.16)/(25) } =0.08`

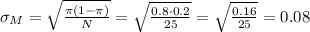
The z value por p=0.6 is

`z=(p-\pi+0.5/N)/(\sigma) =(0.6-0.8+0.5/25)/(0.08)= (-0.18)/(0.08) =-2.25`

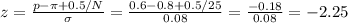
The probability of having a sample mean less than 15 is

`P(\bar X<15)=P(p<0.6)=P(z<-2.25)=0.01222`

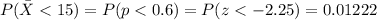
The probaiblity of not rejecting the claim is 1-0.01222=0.98778

If the value 15 is replaced by 14, we have a new value of p=14/25=0.56.

There will be less chances of rejecting the hypothesis.

`z=(p-\pi+0.5/N)/(\sigma) =(0.56-0.8+0.5/25)/(0.08)= (-0.22)/(0.08) =-2.75`

`P(\bar X<14)=P(p<0.56)=P(z<-2.75)=0.00298`