Question

When designing motorcycle helmets, the breadth of a person’s head must be considered. Men have head breadths that are normally distributed with a mean of 6.0 inches and a standard deviation of 1.0 inches. If one male is randomly selected, what is the probability that his head breadth is less than 6.2 inches?

Answer 1

The probability that a randomly selected male's head breadth is less than 6.2 inches is approximately 57.926%.

Step-by-step explanation:

To find the probability that a randomly selected male's head breadth is less than 6.2 inches, we can use the standard normal distribution. First, we calculate the z-score using the formula:

z = (x - mean) / standard deviation

Plugging in the values, we get z = (6.2 - 6.0) / 1.0 = 0.2. Now, we can use a z-table or a calculator to find the probability that a z-score is less than 0.2. The probability is approximately 0.57926, or 57.926%.

Answer 2

57.93%

Step-by-step explanation:

We have been given that men have head breadths that are normally distributed with a mean of 6.0 inches and a standard deviation of 1.0 inches. We are asked to find the probability that a man's breadth is less than 6.2 inches.

First of all, we will find z-score corresponding to sample score of 6.2 as:

`z=(x-\mu)/(\sigma)`, where,

z = Z-score,

x = Sample score,

`\mu` = Mean,

`\sigma` = Standard deviation.

Upon substituting our given values in z-score formula, we will get:

`z=(6.2-6.0)/(1.0)`

`z=(0.2)/(1.0)`

`z=0.2`

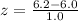
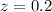
Now, we need to find the probability that a z-score is less than 0.2.

Using normal distribution table, we will get:

`P(z<0.2)=0.57926`

`0.57926\approx 57.926\%\approx 57.93\%`

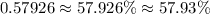
Therefore, the probability that a male's head breadth is less than 6.2 inches, would be approximately 57.93%.