Answer:
Explanation:
Given that an urn consists of 20 red balls and 30 green balls. We choose 10 balls at random from the urn. The sampling is done without replacement (repetition not allowed).
a) The probability that there will be exactly 4 red balls among the chosen balls
= no of ways of selecting 4 red balls and 6 green balls/total number of selecting 10 balls from 30 green balls
=

b) Let A = atleast 3 red balls
B = 4 red balls
Required prob= P(B/A) = P(AB) / P(A)
P(AB) = P(4 red balls)=0.2801
P(A) = P(atleast 3 red balls)
= 1-P(0 or 1 or 2 red ball)
=
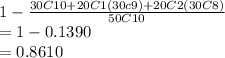
Required prob =
