Question

The manager of an online shop wants to determine whether the mean length of calling time of its customers is significantly more than 3 minutes. A random sample of 100 customers was taken. The average length of calling time in the sample was 3.1 minutes with a standard deviation of 0.5 minutes. At a 0.05 level of significance, it can be concluded that the mean of the population is?

a. significantly less than 3.
b. significantly greater than 3.
c. not significantly greater than 3.
d. not significantly different from 3.10.

Answer 1

the mean of the population is?

b. significantly greater than 3.

Explanation:

Given that the manager of an online shop wants to determine whether the mean length of calling time of its customers is significantly more than 3 minutes

H0:
`\bar x = 3\\`

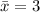
H1:
`\bar x >3\\`

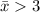
(Right tailed test for checking mean)

n = Sample size = 100

Sample mean = 3.1

s = Sample std dev = 0.5

Std error of mean =
`(s)/(√(n) ) \\=0.05`

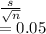
Mean difference = 0.10

Since only sample std dev is used, we can use t test only

t = mean diff/std error =
`(0.1)/(0.05) \\=2`

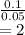
df = 99

p value = 0.02412

Since p < 0.05 our significant level, we reject null hypothesis

The conclusion is

the mean of the population is?

b. significantly greater than 3.