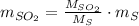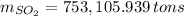Answer:
a)
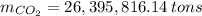 , b)
, b)
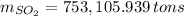
Step-by-step explanation:
a) Number of tons of carbon dioxide produced by the plant throughout the year:
A complete combustion means that a mole of
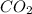 is produced by a mole of
is produced by a mole of
 contained in coal. The yearly burnt carbon is:
contained in coal. The yearly burnt carbon is:

The amount of the yearly
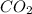 emission is obtained:
emission is obtained:
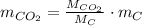
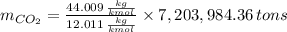
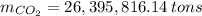
b) Number of tons of tons of sulfur dioxide produced by the plant throughout the year:
The required information is found by applying the same approach seen on previous question. A complete combustion means that a mole of
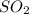 is produced by a mole of
is produced by a mole of
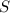 contained in coal.
contained in coal.
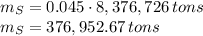
The amount of the yearly
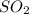 emission is obtained:
emission is obtained: