Question

A pharmaceutical company receives large shipments of aspirin tablets. The acceptance sampling plan is to randomly select and test 47 ​tablets, then accept the whole batch if there is only one or none that​ doesn't meet the required specifications. If one shipment of 3000 aspirin tablets actually has a 3​% rate of​ defects, what is the probability that this whole shipment will be​ accepted? Will almost all such shipments be​ accepted, or will many be​ rejected?

Answer 1

The probability that the whole shipment will be​ accepted is 0.5862.

Explanation:

Let X = number of the aspirin tablets that doesn't meet the required specifications.

The probability of the random variable X is, P (X) = p = 0.03.

The sample of n = 47 tablets are tested from each batch.

The probability of any of the tablets being defective is independent of the others.

The probability mass function of X is,

`P(X=x)={n\choose x}p^(x)(1-)^(n-x);\ x=0,1,2,3...`

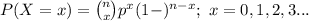
Compute the probability that the whole shipment of 3000 tablets will be​ accepted as follows:

P (X ≤ 1) = P (X = 0) + P (X = 1)

`={47\choose 0}0.03^(0)(1-0.03)^(47-0)+{47\choose 1}0.03^(1)(1-0.03)^(47-1)\\=0.2389+0.3473\\=0.5862`

Thus, the probability that the whole shipment will be​ accepted is 0.5862.

The sample of 47 tablets is significantly small when drawn from a population of 3000 tablets. So it is difficult to make conclusion about all such shipments of aspirin tablets.