Question

A general can plan a campaign to fight one major battle or three small battles. He believes that he has probability .56 of winning the large battle and probability .78 of winning each of the small battles. Assume that victories or defeats in the small battles are independent. The general must win either the large battle or all three small battles to win the campaign. Which strategy should he choose?

Answer 1

Answer: Fight one big battle instead of fight small three battles.

Explanation:

Since we have given that

Probability of winning the large battle = 0.56

Probability of winning each of the small battles = 0.78

Since the victories or defeat in the small battles are independent.

So, Probability of all three small battles to win the campaign is given by

`0.78* 0.78* 0.78\\\\=0.474`

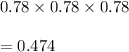
Since 0.56 which is a probability of winning the large battles is more than the probability of winning all three small battles.

So, Large battle would win.

Hence, Fight one big battle instead of fight small three battles.